Understanding LoRA

Posted on

I finally got time to have some deep dives. Happy Christmas!

RAM Usage During Training

Training large-scale machine learning models e.g. LLMs, requires significant compute resources. Here’s a breakdown of the possible memory usage (RAM) at various stages of the classic training process, based on the pseudocode below:

1
2
3
4
5
6
7
8
9
10
11
12
model = Model()
optimizer = Adam(model.parameters())

for batch, (X, y) in enumerate(dataloader):
    # Compute prediction and loss
    pred = model(X)
    loss = loss_fn(pred, y)

    # Backpropagation
    optimizer.zero_grad()
    loss.backward()
    optimizer.step()

Key Components of Memory Usage

  1. Model Parameters: These are the trainable weights of the model, which need to be stored in memory throughout the training process. The size is proportional to the number of parameters in the model.

  2. Model Gradients: Gradients for each parameter are computed during backpropagation and stored temporarily for the optimizer to update the weights.

  3. Optimizer States: Optimizers like Adam maintain additional states, including:

    • First-order momentum: Tracks the moving average of gradients.

    • Second-order momentum: Tracks the moving average of squared gradients.

    • Both momentum terms have the same size as the model gradients.

  4. Activations: Activation outputs from the forward pass are stored for use during backpropagation, where the Hessian matrix is multiplied with the activations. The memory required for activations can be substantial, especially as batch size increases. While the size of parameters, gradients, and optimizer states remains constant, activation memory scales directly with batch size.

  5. Other Overheads: Temporary buffers and memory fragmentation during computation also contribute to RAM usage.

Memory Calculation Examples

  1. Gradients and Parameters:

    For 70B model, using 32-bit floating-point precision (FP32): \[ 70\times10^9\times4 \text{ bytes}\times2 =521.5\text{GM} \] This accounts for the weights and their corresponding gradients.

  2. Optimizer State:

    Adam optimizer requires two additional states (first and second-order momentum), each the same size as the gradients: \[ 70\times10^9\times4 \text{ byte}\times2 =521.5\text{GM} \]

  3. Activations:

    For 70B model with a hidden size of 8192, 80 layers, and FP32 precision, each token’s activation memory: \[ 8192\times80\times4\times12 \text{ bytes/token}=30\text{ MB/token} \]

Simple Strategies for Reducing Memory Usage

  1. Activation Checkpointing: Instead of storing all activation outputs, recompute activations during backpropagation as needed. This significantly reduces activation memory at the cost of additional compute time.
  2. Mixed Precision Training (FP16): Use 16-bit floating-point precision (FP16) instead of FP32 for model weights, gradients, and activations. This halves the memory requirements without substantial accuracy loss when done correctly.

LoRA

Adapters

The original adapter was introduced in 2019 in the paper "Parameter-Efficient Transfer Learning for NLP". It's a small, additional module added to a pre-trained model to adapt it to a new task without significantly changing the original model parameters.

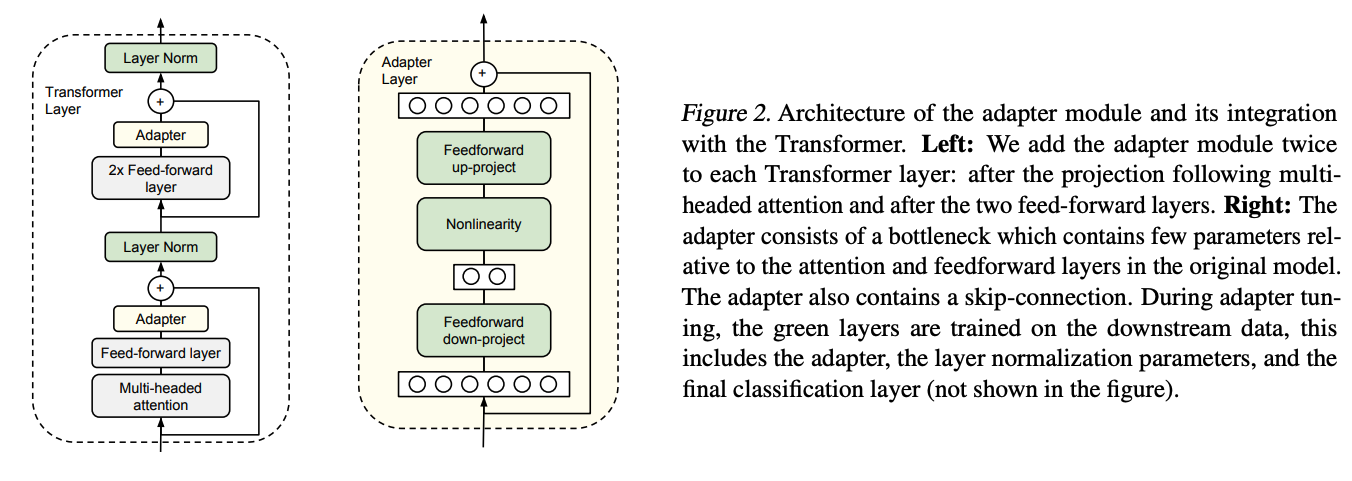
adapter_architecture

Adapters generally reduce training latency compared to full fine-tuning because only a small number of parameters (those within the adapter modules) are updated during training. This reduction in trainable parameters leads to lower computational overhead and faster convergence in many cases. Additionally, adapters allow for larger batch sizes due to reduced memory usage, which can further accelerate training

However, adapter layers increase inference latency because they are added sequentially and cannot be parallelized. This issue becomes more pronounced with small batch sizes or when using sharded models, such as GPT-2. Techniques like layer pruning or multi-task settings can mitigate but not completely eliminate this latency.

As shown in the experiment results below, inference latent can be significant (Source: LoRA paper):

adapter_experiment_results

LoRA Basics

LoRA (Low-Rank Adaptation) was introduced by a Microsoft team in 2021 in the paper LoRA: Low-Rank Adaptation of Large Language Models. The main idea of LoRA is to enable efficient fine-tuning of large pre-trained models by introducing low-rank trainable matrices into the model’s architecture, while keeping the original model weights frozen. This approach significantly reduces the number of trainable parameters and computational requirements compared to full fine-tuning, without compromising performance.

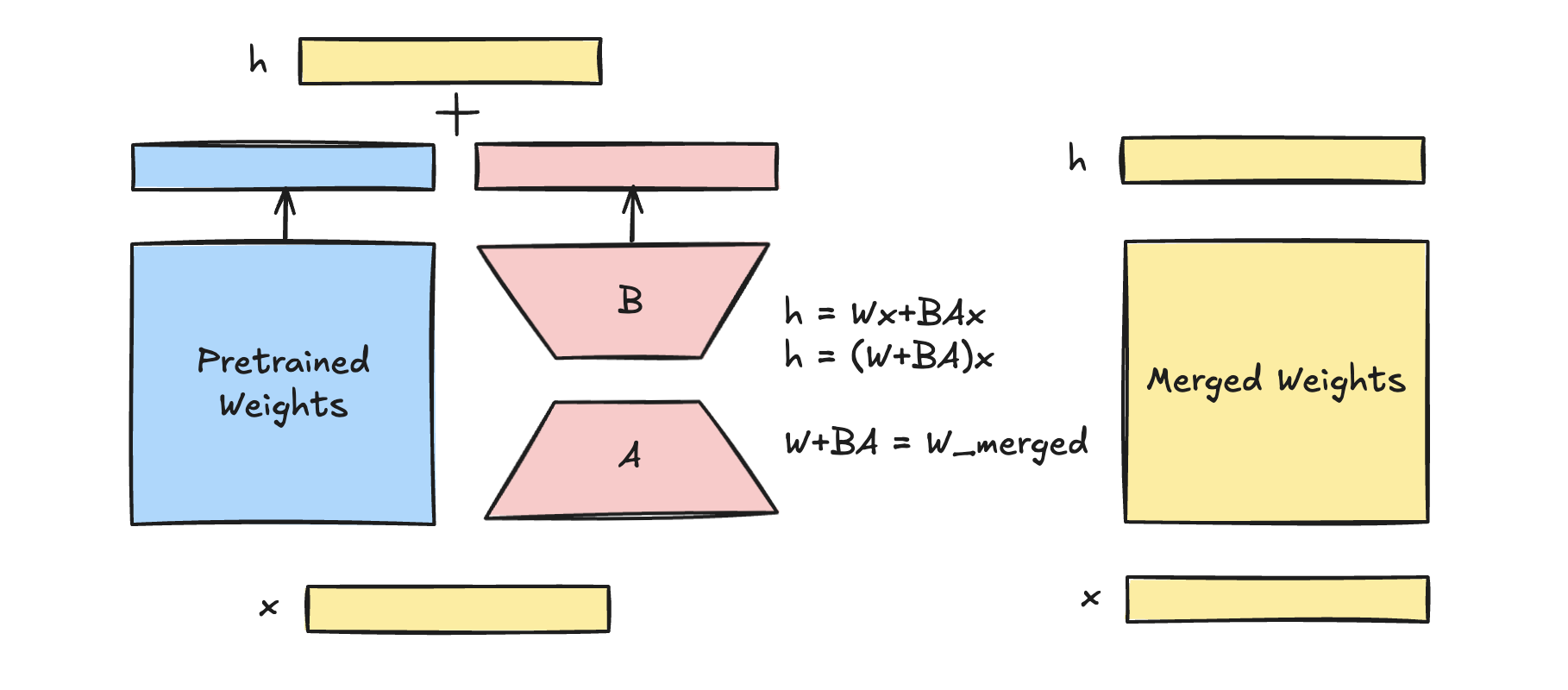
lora_diagram

LoRA approximates weight updates in neural networks using low-rank matrix factorization. Instead of updating the full weight matrix \(W\) , it introduces two smaller trainable matrices \(A\) and \(B\) with size \((r \times d)\) and \((d \times r)\). These matrices have much fewer parameters, as their rank \(r\) is much smaller than the dimensions of \(W\). Instead of training \(\Delta W\), LoRA trains the parameters in \(A\) and \(B\). This can be written in formula: \[ h=W_0x + \Delta Wx = W_0x + BAx \] where \(W_0\) is original prerained weight matrix in size \((d\times d)\) which is frozen during training; \(\Delta W\) is in \((d \times d)\) as well computed by \(BA\). \(x\) is a new input with size \((1 \times d)\).

At the start of the training process, the matrix $ A $ is randomly initialized following a normal distribution \(\mathcal{N}(0, \sigma^2)\), while the matrix $ B $ is initialized as a zero matrix. In the initial round, this setup results in $ BA = 0 $, leading to $ h = W_0x $. This initialization strategy ensures stability by preventing significant deviations of $ W_0 $ from its original state.

LoRA is a groundbreaking method with a lot of benefits:

  • Parameter Efficiency: By training only the low-rank matrices, LoRA reduces the number of updated parameters resulting in lower memory usage and faster training.
  • Frozen Pre-trained Weights: The original pre-trained weights remain unchanged, preserving the model’s general-purpose knowledge and avoiding catastrophic forgetting.
  • No Inference Latency Overhead: Unlike adapters, LoRA does not add additional layers to the model. The low-rank matrices can be merged back into the original weight matrix after fine-tuning, ensuring no additional inference latency.
  • Versatility: LoRA can be applied to various architectures (e.g. transformers) and tasks, making it a flexible solution for adapting large models like GPT-3 or RoBERTa to specific use cases.

LoRA Usage

The Microsoft developers of LoRA created a Python package called loralib to facilitate the use of LoRA. With this library, any linear layer implemented as nn.Linear() can be replaced by lora.Linear(). This is possible because LoRA is designed to work with any layer involving matrix multiplication. The lora.Linear() module introduces a pair of low-rank adaptation matrices, which are used to modify the original weight matrix by applying a low-rank decomposition.

1
2
3
4
5
6
# ===== Before =====
# layer = nn.Linear(in_features, out_features)
# ===== After ======
import loralib as lora
# Add a pair of low-rank adaptation matrices with rank r=16
layer = lora.Linear(in_features, out_features, r=16)

Before training the model, all non-lora matrix should be fixed and only LoRA matrices should be set as trainable. Training loops can run as usual.

1
2
3
4
5
6
7
import loralib as lora
model = BigModel()
# This sets requires_grad to False for all parameters without the string "lora_" in their names
lora.mark_only_lora_as_trainable(model)
# Training loop
for batch in dataloader:
   ...

When saving model checkpoints during LoRA fine-tuning, only the LoRA-specific parameters need to be saved, not the entire large pre-trained model. This results in significantly smaller checkpoint files and more efficient storage.

1
2
3
4
# ===== Before =====
# torch.save(model.state_dict(), checkpoint_path)
# ===== After =====
torch.save(lora.lora_state_dict(model), checkpoint_path)

Implementation of LoRA - lora.Linear()

Let's take a deep dive into the lora.Linear() source code:

The lora.Linear class builds upon torch.nn.Linear(). It retains the original weight matrix $ W $ as initialized in nn.Linear.__init__(self, in_features, out_features), and introduces two additional LoRA matrices: self.lora_A and self.lora_B. The matrix self.lora_A has dimensions of $ (r, ) $, while self.lora_B has dimensions of $ (, r) $. These matrices are used to adapt the original weight matrix through low-rank decomposition.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Linear(nn.Linear, LoRALayer):
    # LoRA implemented in a dense layer
    def __init__(
        self, 
        in_features: int, 
        out_features: int, 
        r: int = 0, 
        lora_alpha: int = 1, 
        lora_dropout: float = 0.,
        fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
        merge_weights: bool = True,
        **kwargs
    ):
        nn.Linear.__init__(self, in_features, out_features, **kwargs)
        LoRALayer.__init__(self, r=r, lora_alpha=lora_alpha, lora_dropout=lora_dropout,
                           merge_weights=merge_weights)

        self.fan_in_fan_out = fan_in_fan_out
        # Actual trainable parameters
        if r > 0:
            self.lora_A = nn.Parameter(self.weight.new_zeros((r, in_features)))
            self.lora_B = nn.Parameter(self.weight.new_zeros((out_features, r)))
            self.scaling = self.lora_alpha / self.r
            # Freezing the pre-trained weight matrix
            self.weight.requires_grad = False
        self.reset_parameters()
        if fan_in_fan_out:
            self.weight.data = self.weight.data.transpose(0, 1)

In the forward() function, it implements \(h=W_0x + \Delta Wx = W_0x+ BAx\).

There is a flag variable called self.merge which is use to flag whether it's doing inference or training. Recall that the original weight matrix remaining unchanged during LoRA training is a key feature of the LoRA - pre-trained weights are freezed and instead small, low-rank matrices are trained to approximate updates.

  • During inference, if merge_weights is set to True, the low-rank updates self.lora_B @ self.lora_A are added directly to the frozen pre-trained weights (self.weight). This avoids the need for separate computations of LoRA updates during forward passes, improving efficiency.
  • During training, if merge_weights is enabled and weights were previously merged, the updates are subtracted from self.weight to revert it to its original frozen state. This ensures that gradients are not incorrectly computed on the merged weights.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Linear(nn.Linear, LoRALayer):
    # LoRA implemented in a dense layer
    def __init__(
        self, 
        in_features: int, 
        out_features: int, 
        r: int = 0, 
        lora_alpha: int = 1, 
        lora_dropout: float = 0.,
        fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
        merge_weights: bool = True,
        **kwargs
    ):

      ......
      
    def train(self, mode: bool = True):
        def T(w):
            return w.transpose(0, 1) if self.fan_in_fan_out else w
        nn.Linear.train(self, mode)
        if mode:
            if self.merge_weights and self.merged:
                # Make sure that the weights are not merged
                if self.r > 0:
                    self.weight.data -= T(self.lora_B @ self.lora_A) * self.scaling
                self.merged = False
        else:
            if self.merge_weights and not self.merged:
                # Merge the weights and mark it
                if self.r > 0:
                    self.weight.data += T(self.lora_B @ self.lora_A) * self.scaling
                self.merged = True    
                
			def forward(self, x: torch.Tensor):
        def T(w):
            return w.transpose(0, 1) if self.fan_in_fan_out else w
        if self.r > 0 and not self.merged:
            result = F.linear(x, T(self.weight), bias=self.bias)            
            result += (self.lora_dropout(x) @ self.lora_A.transpose(0, 1) @ self.lora_B.transpose(0, 1)) * self.scaling
            return result
        else:
            return F.linear(x, T(self.weight), bias=self.bias)
          
      ......